In Python, there are different types of operators are there which help us in carrying out different operations from arithmetic to comparison and from identity to membership operations.
These operators use special symbols and reserved keywords to perform specific operations on values and variables.
Operators that operate on a value are known as operands.
Like these operators, Python has a built-in operator that operates on bits.
Introduction
Like all the operators in Python, there are Bitwise Operators that are used to perform the bitwise calculations on the integer values.
As it depicts from its name, this operator converts the integer values into the binary format and then performs bit by bit operation on it and again returns the result in decimal format.
Why convert it into a binary format?
There are 2 types of number systems:
- Denary (0 – 9)
- Binary (0 and 1)
Well, we humans understand and use the number system that has ten digits (0-9) in our everyday life. But what about computers? So computers work by manipulating 1s and 0s and these are binary digits, or bits for short.
Now you’ve got the idea that to perform the bitwise calculation on integer values, the computer translates into 1s and 0s which is pretty understandable by the computers.
There are 6 types of Bitwise operations:
| Operator | Description | Syntax |
& | Bitwise AND | x & y |
| | Bitwise OR | x | y |
~ | Bitwise NOT | ~x |
^ | Bitwise XOR | x ^ y |
>> | Bitwise right shift | x>> |
<< | Bitwise left shift | x<< |
Let’s discuss them one by one.
Note: Bitwise operator works only on int (integer) type otherwise TypeError will be raised.
Bitwise AND operator
Bitwise AND operators are represented by the “&” (ampersand) sign.
When we perform the Bitwise AND operation on values it returns 1 if both the bits are 1 else it will return 0.
|
1 2 3 4 5 6 7 |
x = 5 # 0101 (binary) y = 6 # 0110 (binary) output = x & y print(output) >>> 4 |
The output will be 4.
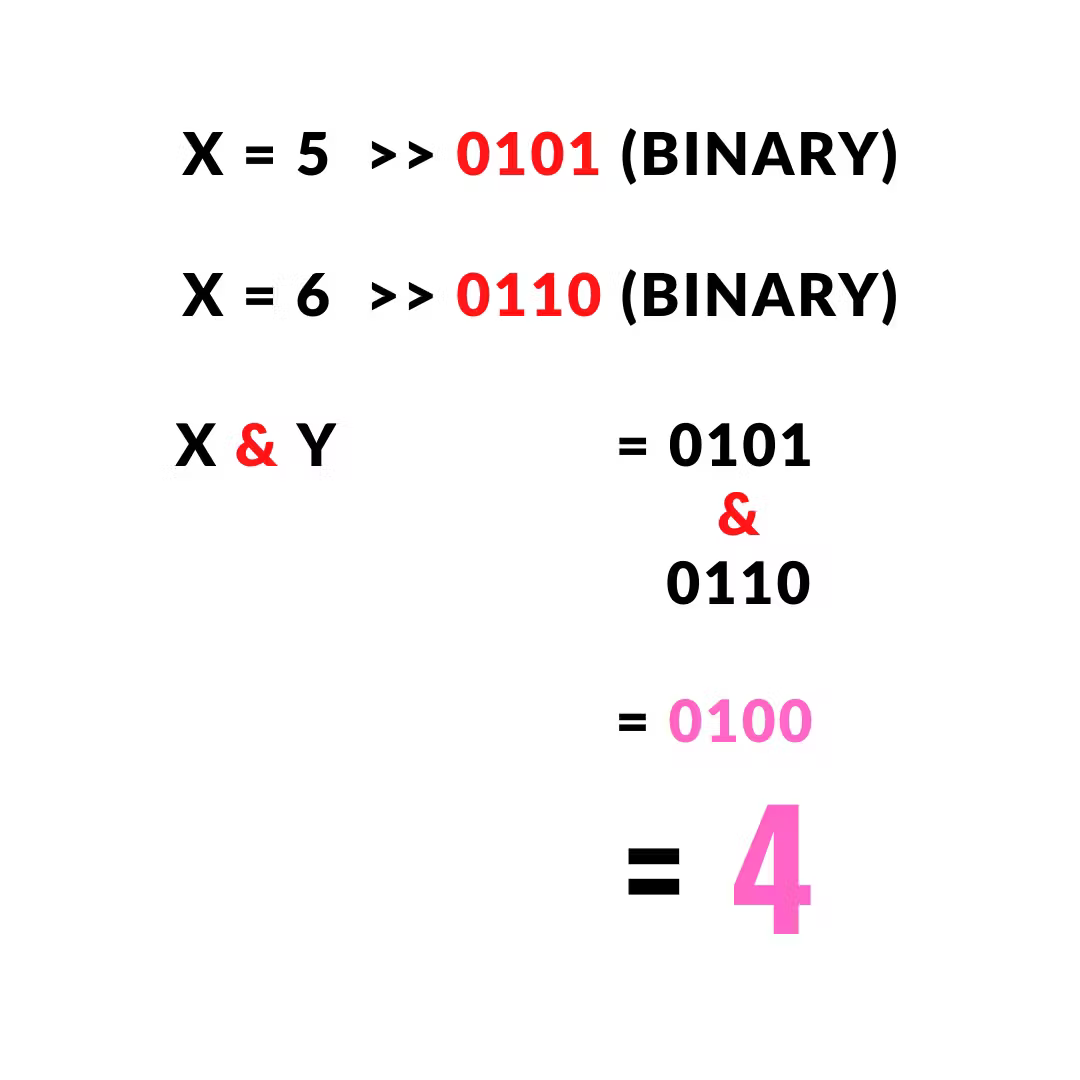
There you can see that it returns 1 when the binary digits at 2nd index from right both are 1 and returns 0 when either of the bits is 0 and the other is 1.
If we see it arithmetically, then the equation is

Here, x and y are the integer values that are converted into binary format, and index is the index number of binary digits.
If we try to gain results using this equation, so the process will be
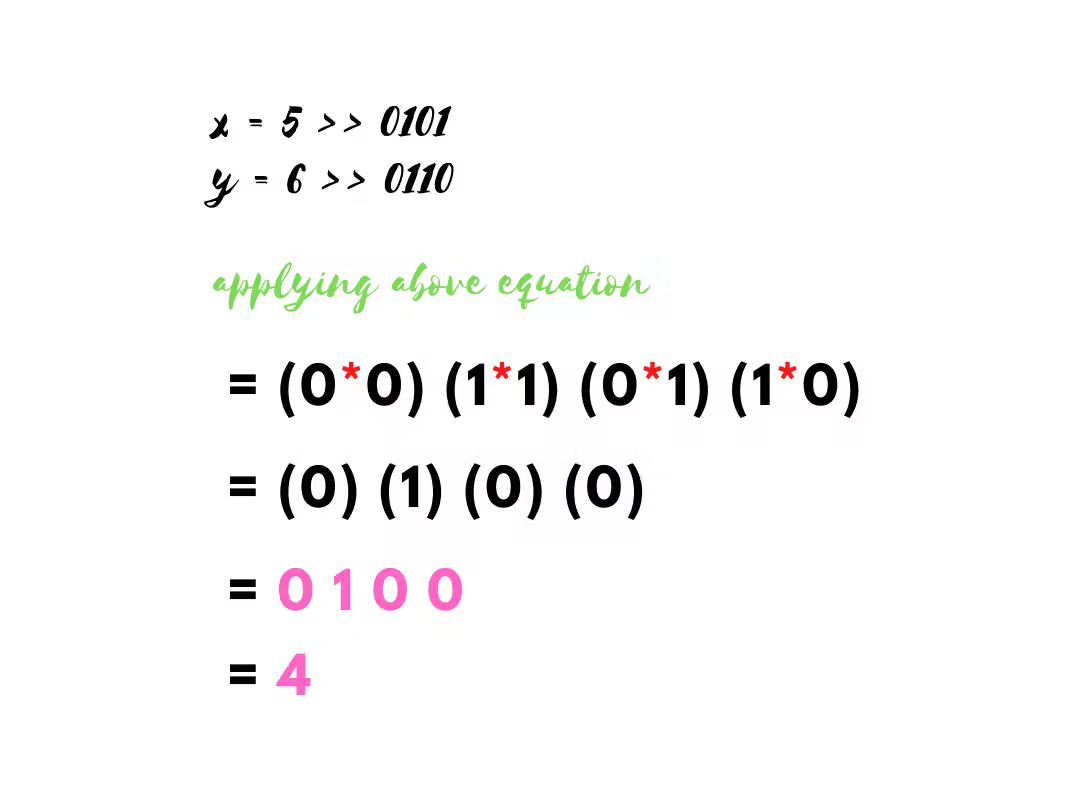
Now you got a pretty good idea of what is happening behind the scenes.
Bitwise OR operator
Bitwise OR operators are represented by the “|” (pipe) sign.
Bitwise OR operator returns 1 if any of the bits is 1 else it will return 0.
|
1 2 3 4 5 6 7 |
x = 5 # 0101 (binary) y = 6 # 0110 (binary) output = x | y print(output) >>> 7 |
The output will be 7
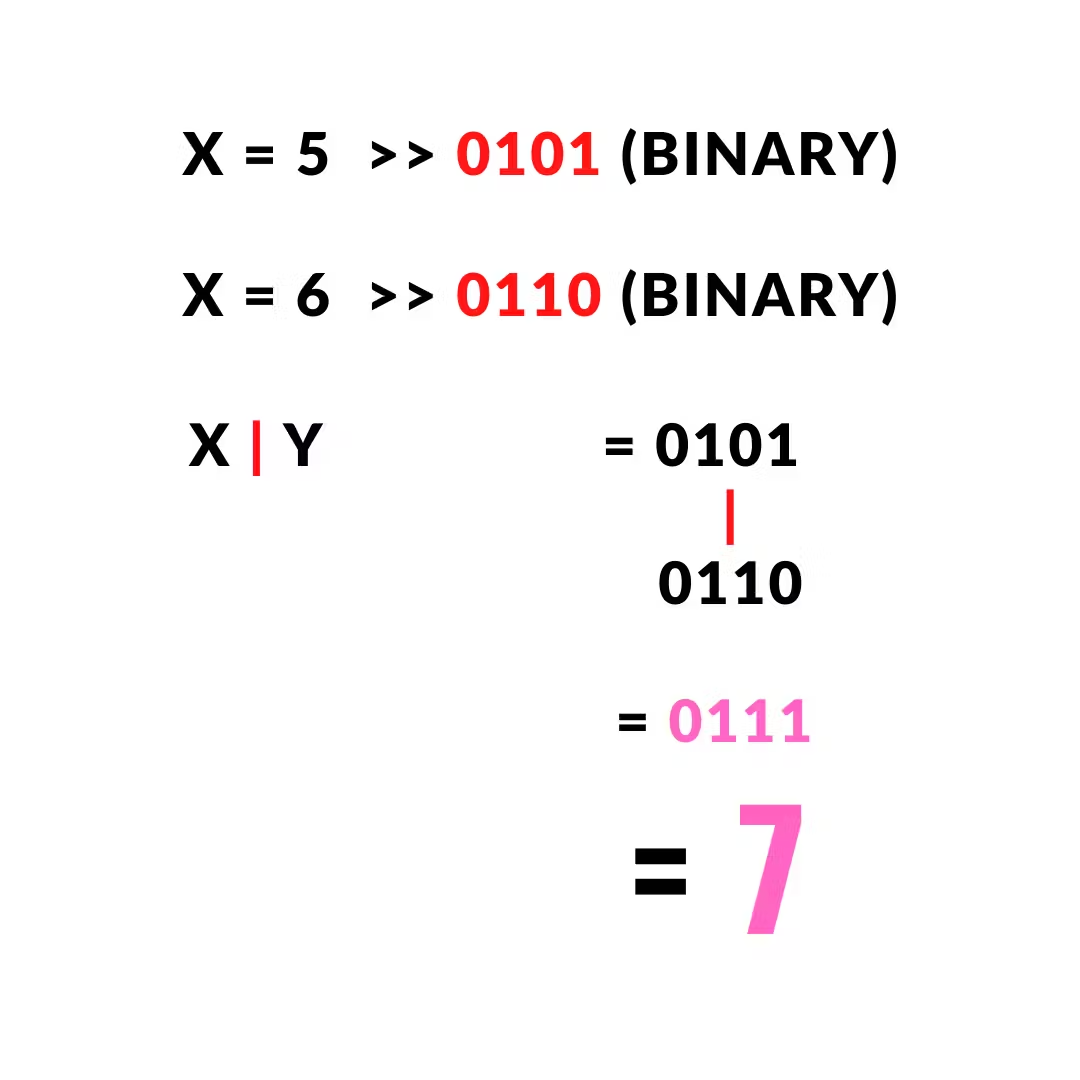
Here, it returns 1 when either of the bits is 1 else returned 0.
Arithmetic equation

Performing equation on binary digit

Here we performed a simple arithmetic operation.
Bitwise NOT operator
Bitwise NOT operators are represented by the “~” (invert) sign.
It uses the unary ( ~ ) invert operator and inverts all the bits.
The result is returned after performing this equation
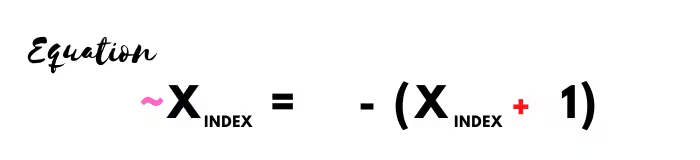
|
1 2 3 4 5 6 |
x = 5 # 0101 (binary) output = ~x print(output) >>> -6 |
As you already saw the equation above, let’s see how it happened behind the scene
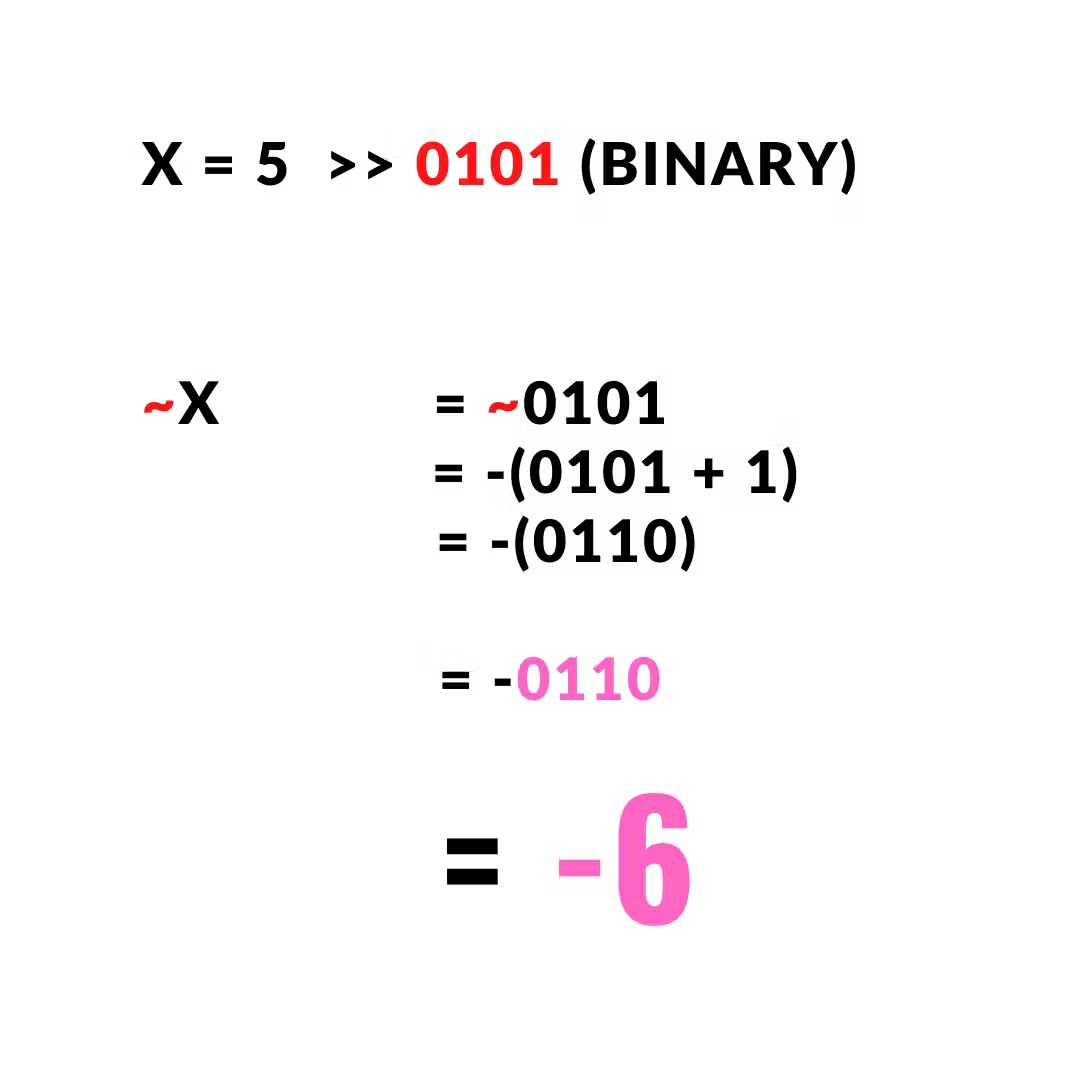
Now if you are wondering how 0101 + 1 = 0110 why not 0101 + 1 = 0102?
If we add 1 + 1 in binary then we’ll get 10.
Binary addition only has three rules:
- 0 + 0 = 0
- 0 + 1 = 1 or 1 + 0 = 1
- 1 + 1 = 10 Source
If we see it arithmetically then the process will be the same as above.

Bitwise XOR operator
Bitwise XOR operators are represented by the “^” (circumflex) sign.
Bitwise XOR operator returns 1 if either of the bit is 0 and the other bit is 1 else it will return 0 if both the bits are the same i.e., both the bits are 0 or 1.
|
1 2 3 4 5 6 7 |
x = 5 # 0101 (binary) y = 6 # 0110 (binary) output = x ^ y print(output) >>> 3 |
The output will be 3
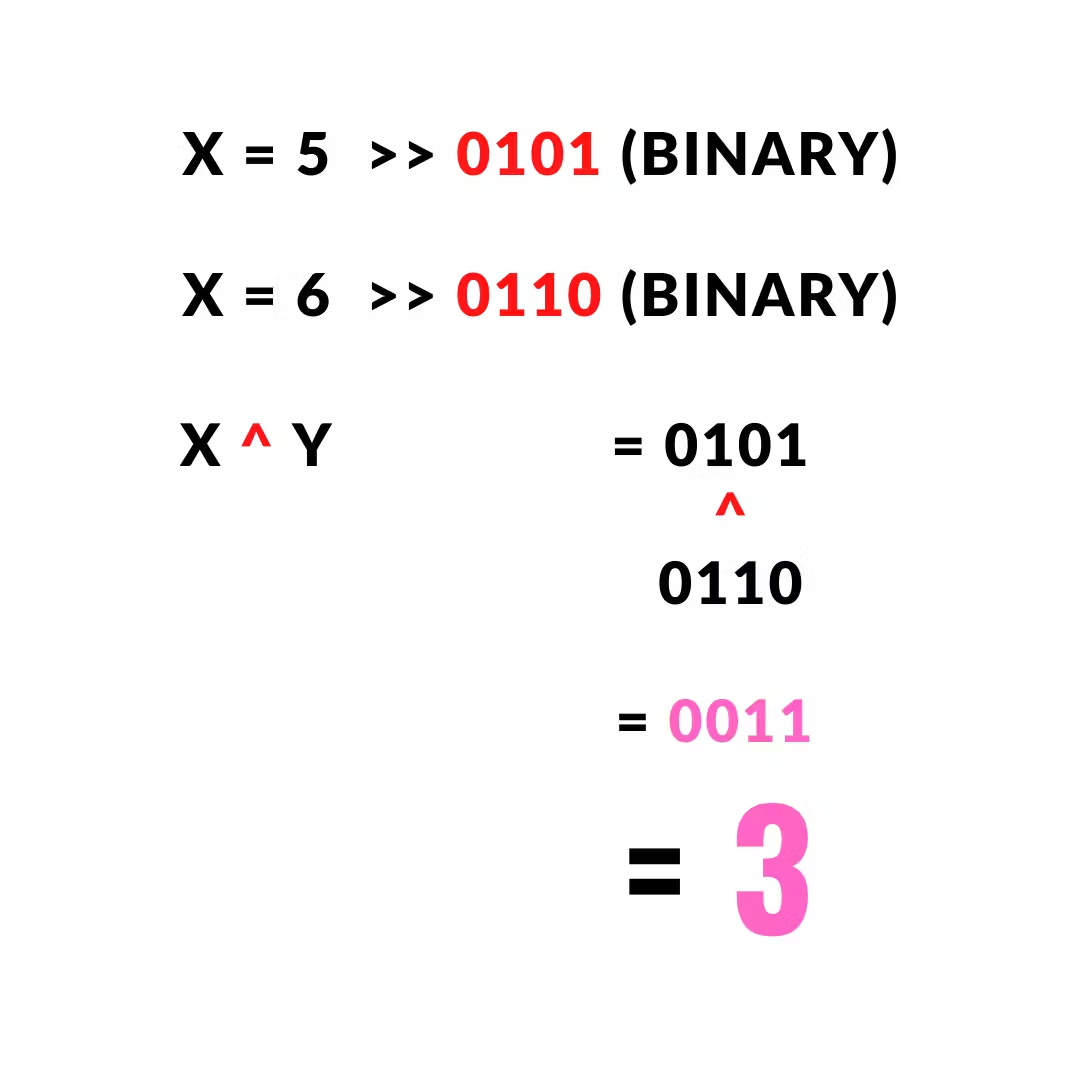
The arithmetic equation will be

The equation looks pretty simple but one thing to keep in mind is the ( % ) sign there is not for calculating the percentage of the value, it is modulo that returns the remainder of the Dividend and the Divisor.
Python has a built-in modulo operator.
The % (modulo) operator yields the remainder from the division of the first argument by the second. The numeric arguments are first converted to a common type. Source
Let’s see how to do it to get the result

Here you can see we got 1 when we perform 1 % 2 (1 modulo 2). When we perform simple division then we get 0.5 as quotient and the remainder will be 0 but when we perform 1 % 2 in Python then we’ll get 1 in the console.
Give it a try in your Python program.
Bitwise Left Shift operator
Bitwise left shift operators are represented by the “<<“ sign.
If you look carefully, then you’ll see it like it is indicating to shift left. Well, it does the same as it is looking.
Bitwise left shift operator shifts the left operand to the left, the number of times specified in the right operand.
In simple terminology, the specified number of 0s is appended at the end of the binary number.
|
1 2 3 4 5 6 |
x = 5 # 0101 (binary) output = x<<2 print(output) >>> 20 |
The output will be 20.
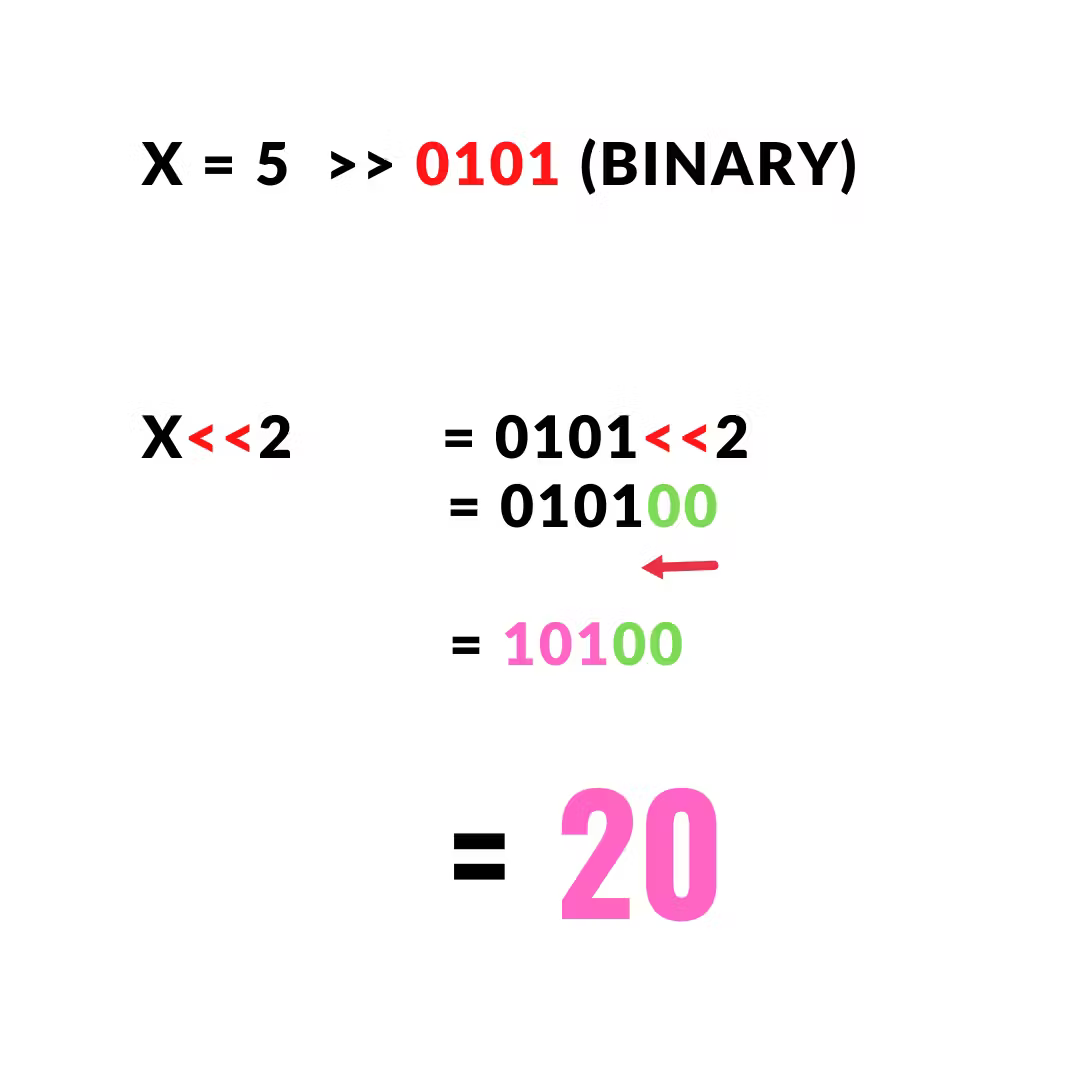
In the above example, 00 (2) zeros are appended at the end by shifting the binary digit to the left.
It also has an equation and we can get results by doing it arithmetically
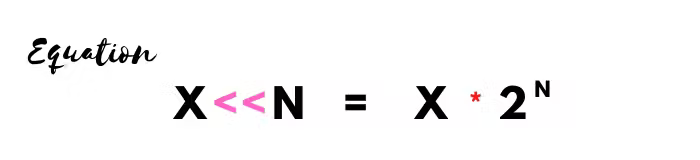
Here x is a binary digit and n is the number of times to be shifted.
Arithmetically, the binary digit is multiplied by the 2 raised to the power n.
If we try to gain results arithmetically, then the process will be
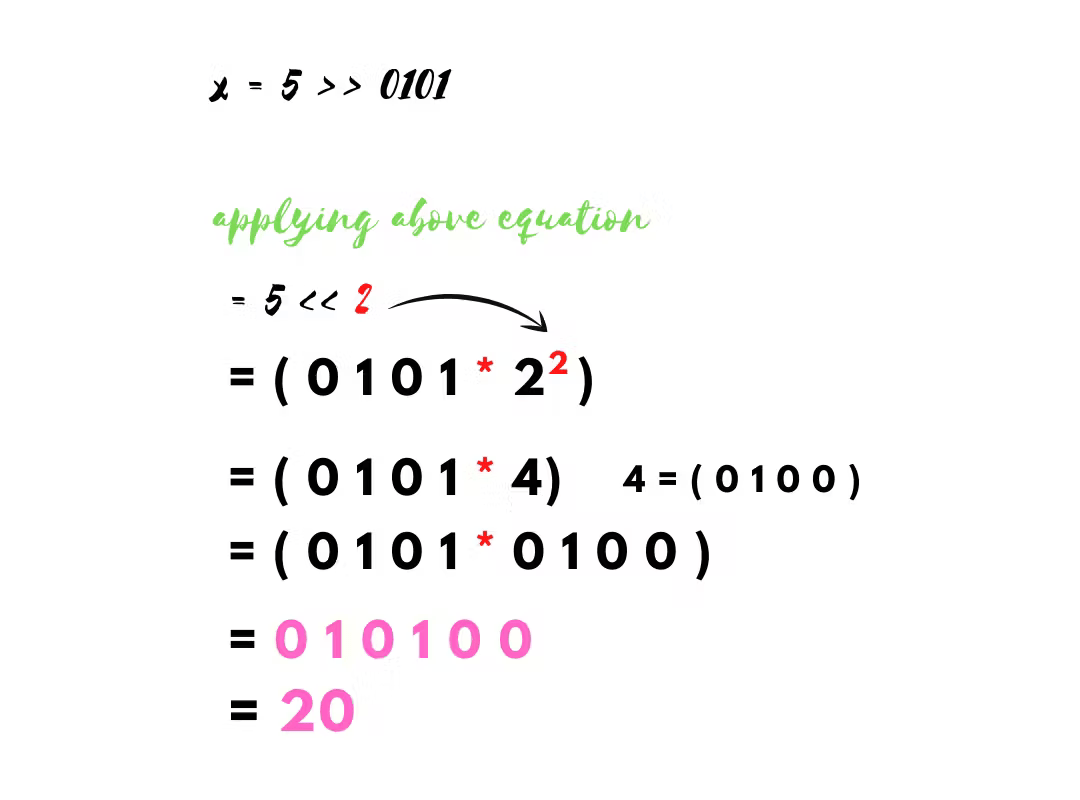
If you are unable to understand the multiplication of binary digits then refer to the articles on google.
Bitwise Right Shift operator
Bitwise right shift operators are represented by the “>>” sign.
If you look carefully, then you’ll see it like it is indicating to shift right. Well, it does the same as it is looking.
Bitwise right shift operator shifts the left operand to the right, the number of times specified in the right operand.
In simple terminology, right side bits are removed.
|
1 2 3 4 5 6 |
x = 5 # 0101 (binary) output = x>>2 print(output) >>> 1 |
The output will be 1
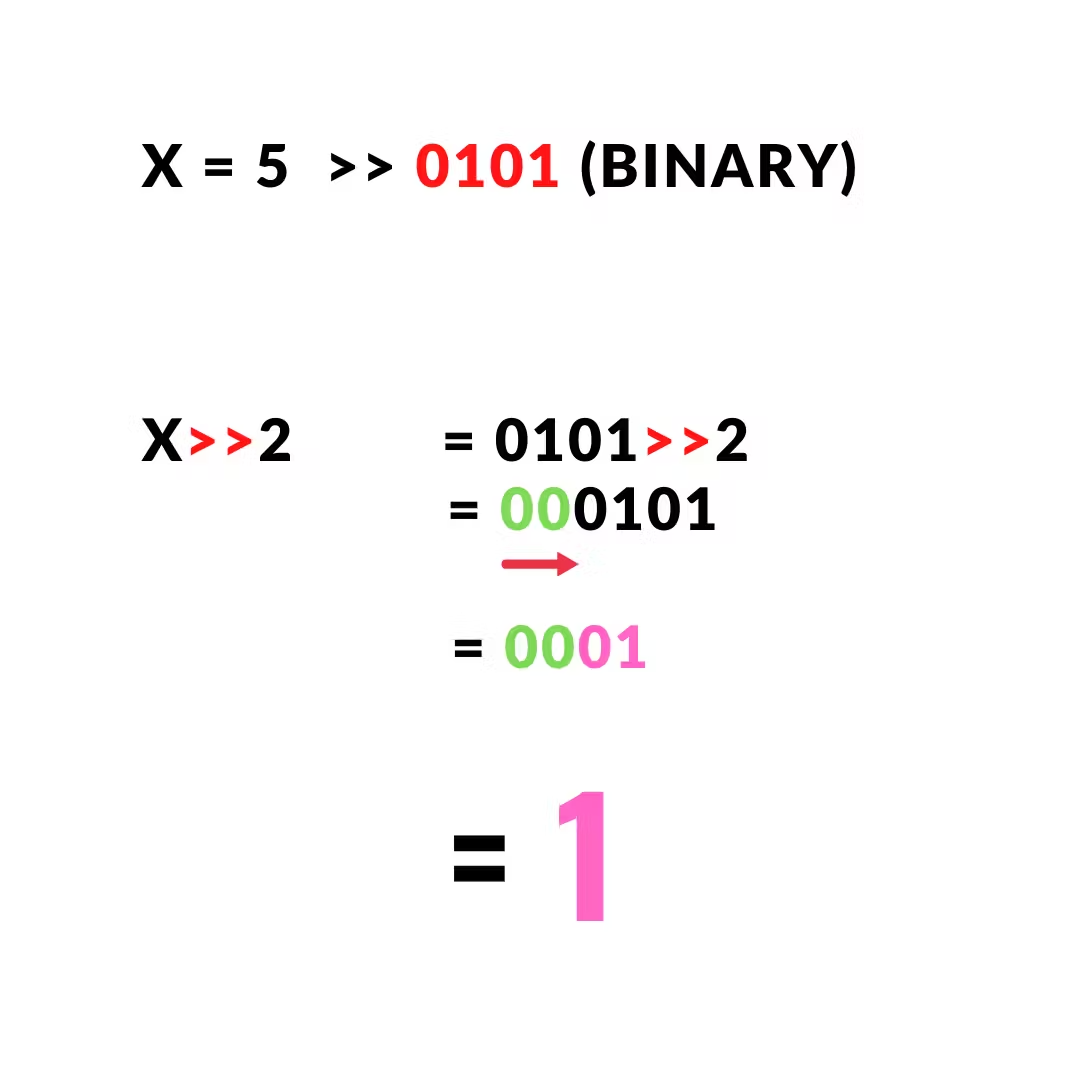
Well if we see the equation, it is a bit different from the left shift operator equation
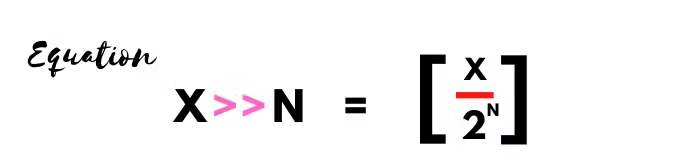
In the left shift operator equation, we multiplied the binary digit from 2 raised to the power n, we are doing the same thing here but instead of multiplying we are dividing.
Let’s see how we can perform it arithmetically
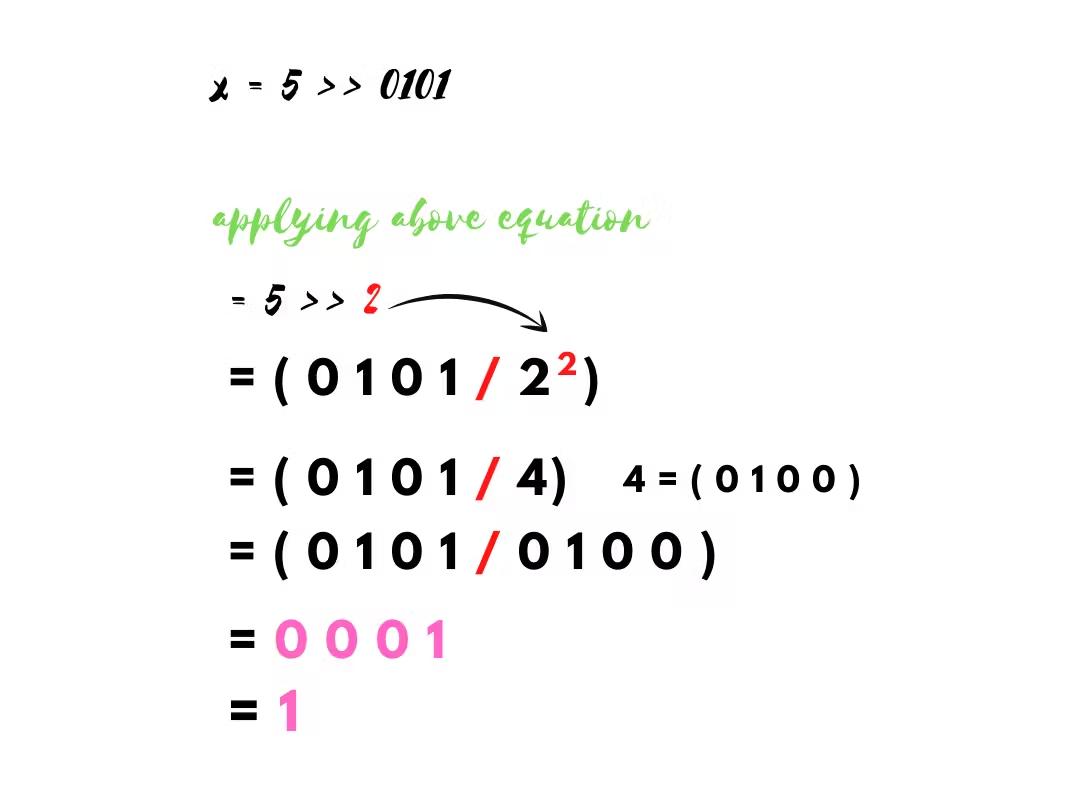
If you don’t know how to divide the binary digits then refer to the relevant articles.
Conclusion
You have learned what can bitwise operators do and how they run equations behind the scenes.
Understanding Bitwise operations lets you unlock your knowledge to manipulate binary digits using different bitwise operators in your Python code.
Go ahead and start working on binary numbers in your Python program and make good use of your knowledge.
That’s all for this article
Keep Coding✌✌